数据结构实验五：二叉树

发表于 | 分类于 | 评论数： | 阅读次数：
本文字数： 8k | 阅读时长 ≈ 15 分钟

实验五 二叉树

一、实验目的

（1）熟悉链栈的定义和基本操作。

（2）熟练掌握二叉树的定义和基本操作。

二、实验内容 结点存放整数的二叉树结构定义如下： Typedef struct biTrNode{ int data; int *left, *right; }BiTrNode, *BTree; 编制一C程序，实现如下操作：

  1. 构造一个函数createBTree（），该函数的功能如其名所示，它从键盘接收整数输入，然后根据输入的整数构造一个二叉树。具体细节如下：

    1. 如果输入的是正整数，则该数将被存入二叉树的某个结点数据域（data）中，

    2. 如果输入的是整数 -1， 则表示其前面刚输入的正整数的左或右子树为空。例如：输入数组

    2，-1，-1, 0 得到 二叉树：

    输入数组：

    5 4 -1 3 2 -1-1 1 -1 -1 6 -1 7 8 -1 -1 9 -1 -1 0

    得到二叉树

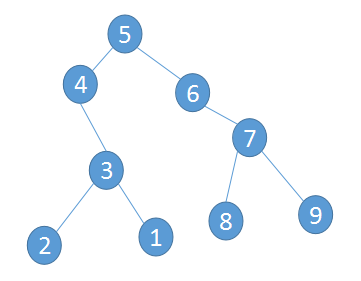
    注： 数组里最后出现的数字0 表示构成该树的所有正整数已输入完毕。

    本操作的算法如下：（非递归先序构造二叉树）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44

    #define DATAEND 0

    #define EMPTY -1

    BTree createBiTreeNonRecursive(void)

    {

    int num; bool keepRun = true;

    BTree treeHead=NULL;

    S= initStack(); //初始化链栈，

    while(keepRun){

    cin>>num;

    switch(num){

    case EMPTY:

    processEmptyData();

    continue;

    case DATAEND:

    processEndData();

    keepRun=false; break;

    default:

    addNode(treeHead, num);

    }

    }

    return treeHead;

    }
    1. 为此你可能需要构造一个链栈： S，其结点构造如下：
      1
      2
      3
      4
      5
      6
      7
      8
      9
      typedef struct StackNode{

      biTrNode* nodePtr;

      char child;

      StackNode* next;

      } *StackPtr;

其中 S 定义为一全局变量： STackPtr S;

并分别实现其压栈、弹栈，取栈顶数据和判断非空等操作。

而三个函数　

addNode(treeHead, num);//算法见如下

processEmptyData();//算法自己设计

processEndData(); //算法需要自己设计

分别用于处理三类不同的数据。其中

addNode(treeHead, num); //这里num 值不为0 和 -1

算法如下：

  1. biTrNode* pt;

  2. If 栈 S 为空，显示出错信息，表明当前没有结点的需要填充孩子结点，然后退出程序。

  3. 申请空间存放二叉树结点p，其data成员赋值为 num；

  4. 从栈S 的栈顶结点（S->next）中取出当前需要补充孩子结点（S->next->nodeptr）的父结点地址，将其放入 pt中。

    1. 从栈顶S->next结点中取出 child值。

    2. 如果其值为”L”,则将p赋值给父结点的left成员，并改child值为”R”; 否则child的值为”R”，需要将p赋值给父结点的right成员，同时弹出栈S的栈顶元素。

    3. 在栈S中压入一新结点，nodePtr 赋值为p，child成员赋值为 “L”.

  1. 实现二叉树的三种遍历算法：DLR, LDR 和 LRD(注：必须实现递归和非递归两种方式遍历）

  2. 用下面的是数据测试你的程序：

  3. 5 4 -1 3 2 -1-1 1 -1 -1 6 -1 7 8 -1 -1 9 -1 -1 0

  4. 3 2 1 0

  5. 1 2 3 -1 -1 4 -1 -1 5 6 8 -1 -1 7 -1 -1 -1 0

    测试输出样例如下图：

  1. 实现求二叉树叶子的操作，并对每个测试的树，显示其叶子数。

  2. 实现求二叉树的深度的操作，并对每个测试的树，显示其深度。

    三、实验要求：
    （1）实验报告中需要显示所建立的抽象数据模型。
    （2）按步骤将程序运行结果截图写入实验报告。
    （3）实验需要在两周内按时完成。
    注：实验报告内容项中可以去掉非递归先序构造二叉树代码部分，其他部分需填在实验报告里。

学习资料:

二叉树：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
#include <iostream>
#include <cstdlib>
#include <stdio.h>
#include <stdlib.h> 
#define OK 1 
#define DATAEND  0
#define EMPTY     -1
#define ERROR  0
typedef  int  ElemType ;
using namespace std;


/***二叉树结构体***/ 
typedef struct BiTrNode{
  int data;
  struct BiTrNode \*left, \*right;
}BiTrNode,  *BTree;

/***链栈***/ 
typedef struct StackNode{
        BiTrNode* nodePtr; 
        char  child;
        StackNode* next;
} *StackPtr;

//StackPtr    S;

 
 
int addNode(BTree &treeHead,int num);
int initStack(StackPtr &S);
BTree createBiTreeNonRecursive(void);
void PreOderTraverse(BTree T);
 
 
/*初始化链栈*/
int InitStack(StackNode &p)    /* 初始化 */
{
    p.next=NULL;
    return OK;
}


/*判断链栈是否为空*/
int StackEmpty(StackNode p)
{
	if(p.next == NULL)return OK;
	else return ERROR;
}


/***压栈***/ 
int push(StackNode &S,BTree e,char c){
	StackPtr p = (StackPtr)malloc(sizeof(StackNode));  //分配空间 
	if(!p)return ERROR;
	p->nodePtr = e;           //nodePtr赋值 
	p->child = c;             //child赋值 
	p->next = S.next;
	S.next = p;
	return OK;
}


/***弹栈***/ 
int pop(StackNode &S)
{
	if(StackEmpty(S))return ERROR;
	S.next = S.next->next;         //改变指针 
	return OK;
}


bool b=false; 

//构造二叉树
void CreateBTree(BTree &BT){
	int data;
	if(b){
		BT = NULL;
		return;
	}
	cin>>data;
	if(data==DATAEND){
		BT=NULL;
		b=true;
	}else if(data==EMPTY){
		BT=NULL;
	}else{
		BT=(BTree)malloc(sizeof(BiTrNode));
		BT->data=data;
		CreateBTree(BT->left);
		CreateBTree(BT->right);
	}
}



/***递归先序遍历二叉树***/
void preOrder_DLR(BTree BT) 
{
	if(BT){
		printf("%-4d",BT->data);    //输出节点数据 
		preOrder_DLR(BT->left);    //递归左子树 
		preOrder_DLR(BT->right);   //递归右子树 
	}
}

/***递归中序遍历二叉树***/
void inOrder_LDR(BTree BT) 
{
	if(BT){
		inOrder_LDR(BT->left);    //递归左子树 
		printf("%-4d",BT->data);    //输出节点数据 
		inOrder_LDR(BT->right);   //递归右子树 
	}
}

/***递归后序遍历二叉树***/
void postOrder_LRD(BTree BT) 
{
	if(BT){
		postOrder_LRD(BT->left);    //递归左子树 
		postOrder_LRD(BT->right);   //递归右子树 
		printf("%-4d",BT->data);    //输出节点数据 
	}
}

/***非递归先序遍历二叉树***/
void NoRecursionPreOrderTraverse_DLR(BTree T)
{
	StackNode S;       //创建栈 
	BTree P=T;         //将树指针赋给p 
	InitStack(S);
	while(P||!StackEmpty(S)){
		while(P){
			printf("%-4d",P->data);    //输出节点数据 
			push(S,P,'L');       //将P入栈S 
			P=P->left;           //p指针指向左子树 
		}
		P=S.next->nodePtr;       //将p指针指向栈s的nodePtr 
		pop(S);                 //S的顶点元素出栈 
		P=P->right;            //将P指向P的右子树 
	}
}

/***非递归中序遍历二叉树***/
void NoRecursionInOrderTraverse_LDR(BTree T)
{
	StackNode S;       //创建栈 
	BTree P=T;         //将树指针赋给p 
	InitStack(S);
	while(P||!StackEmpty(S)){
		while(P){
			
			push(S,P,'L');        //将P入栈S 
			P=P->left;           //p指针指向左子树 
		}
		P=S.next->nodePtr;       //将p指针指向栈s的nodePtr 
		printf("%-4d",P->data);    //输出节点数据 
		pop(S);                 //S的顶点元素出栈 
		P=P->right;            //将P指向P的右子树 
	}
}

/***非递归后序遍历二叉树***/
void NoRecursionPostOrderTraverse_LRD(BTree T)
{
	StackNode S;       //创建栈 
	BTree P=T;         //将树指针赋给p 
	InitStack(S);
	while(T){
		push(S,T,'L');        //将左孩子树入栈
		T = T->left;
	}	 
	while(!StackEmpty(S)){
			P=S.next->nodePtr;
			if(!P->right||S.next->child=='R'){
				printf("%-4d",P->data);    //输出节点数据
				pop(S);                 //S的顶点元素出栈 
				T=P;
			}else{
				T=P;
				P=P->right;            //将P指向P的右子树
				S.next->child='R';
			}
			while(P!=T&&P){
				push(S,P,'L');        //将P入栈S 
				P=P->left;           //p指针指向左子树 
			}
		}
}
int processEmptyData(BTree &treeHead)
{
	
}

void PreOderTraverse(BTree T)
{
    if(T==NULL)
        return;
    cout<<"二叉树这里"; 
    printf("%d",T->data);  //显示结点数据，可以更改为其他对结点操作
    PreOderTraverse(T->left);   //先遍历左子树
    PreOderTraverse(T->right);    //最后遍历右子树 
 } 
int PostOrder(BTree T) {
    if(T){
        PostOrder(T->left);
        PostOrder(T->right);
        printf("%d",T->data);
        return OK;
    }
    else return ERROR;
}

/***计算叶子节点数***/
int Leave(BTree BT)
{
	int ll,lr;
	if(!BT)return 0;
	if(!BT->left&&!BT->right)
		return 1; //判断是否为一个节点的树 
	ll=Leave(BT->left);       //递归左树 
	lr=Leave(BT->right);	  //递归右树 
	return ll+lr; 
} 
 
/***计算树的深度***/
int BTreeDepth(BTree BT)
{
	if(BT==NULL)
		return 0;
	else{
		int dep1=BTreeDepth(BT->left);
		int dep2=BTreeDepth(BT->right);
		if(dep1>dep2)
			return dep1+1;
		else
			return dep2+1; 
		}
 } 
int main()
{
	BTree T;
	cout<<"先序输入二叉树："<<endl;
	CreateBTree(T);
	cout<<"先序递归遍历二叉树："<<endl;
	preOrder_DLR(T);
	cout<<endl;
	cout<<"中序递归遍历二叉树："<<endl;
	inOrder_LDR(T);
	cout<<endl;
	cout<<"后序递归遍历二叉树："<<endl;
	postOrder_LRD(T);
	cout<<endl;
	cout<<"先序非递归遍历二叉树："<<endl;
	NoRecursionPreOrderTraverse_DLR(T);
	cout<<endl;
	cout<<"中序非递归遍历二叉树："<<endl;
	NoRecursionInOrderTraverse_LDR(T);
	cout<<endl;
	cout<<"后序非递归遍历二叉树："<<endl;
	NoRecursionPostOrderTraverse_LRD(T);
	cout<<endl;
	cout<<"该二叉树的叶子结点数为："<<endl;
	cout<<Leave(T)<<endl;
	cout<<endl;
	cout<<"该二叉树的深度为："<<endl;
	cout<<BTreeDepth(T)<<endl;
	return 0;
}

0%